From water bubbling into steam to ice cubes softening in a glass, we’ve all seen the peculiarity known as a “stage change” in our daily existences. Yet, there’s one more kind of stage change that is a lot harder to see, yet comparably obvious: quantum stage changes.
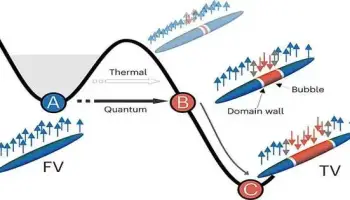
When cooled to approach outright zero, certain materials can go through these quantum stage changes, which can make a physicist’s jaw drop. The material can flip from being attractive to non-attractive, or it can abruptly get the superpower to lead power with zero energy lost as intensity.
The math behind these changes is hard to deal with in any event, for supercomputers—yet another Physical Review A review from the University of Chicago proposes a better approach to working with these muddled estimations, which could ultimately yield mechanical leaps forward. The easy route manipulates just the main data into the situation, and makes a “map” of all conceivable stage changes in the framework being mimicked.
“This approach to studying quantum phase transitions has the potential to be very effective and can be applied to classical or quantum computers.”
David Mazziotti, a theoretical chemist with the Department of Chemistry
“This is a possible strong perspective on stage changes that can be utilized with either customary or quantum PCs,” said David Mazziotti, a hypothetical scientist with the Department of Chemistry and the James Franck Institute at the University of Chicago and senior creator of the review.
He, and other researchers, believe that if we can fully comprehend the perplexing material science at work behind quantum stage changes, we will be able to pave the way for new advances.Comparable disclosures before, for instance, have prompted MRI machines and the semiconductors that make current PCs and telephones conceivable.
A streamlined approach
The stage transforms you know about, like vanishing and buildup, occur because of temperature changes. Yet, quantum stage changes are set off by some impedance in their current circumstance, like an attractive field.
The peculiarity happens because of numerous electrons acting in relationship to each other — a sort of connection that falls under a famously perplexing subfield known as “firmly corresponded” physical science. Generally, to mimic these quantum stage changes, researchers should make a model that integrates the opportunities for each and every electron. Yet, the figurative power expected to run these recreations gains influence rapidly.
For instance, quantum PCs are believed to be better suited for this sort of issue than ordinary PCs, yet even this strategy has its snags: for instance, these issues generate a lot of information that then should be made an interpretation of back into the language of “normal” PCs for researchers to work with them.
So the analysts needed to perceive how they could work on the estimation without losing exactness.
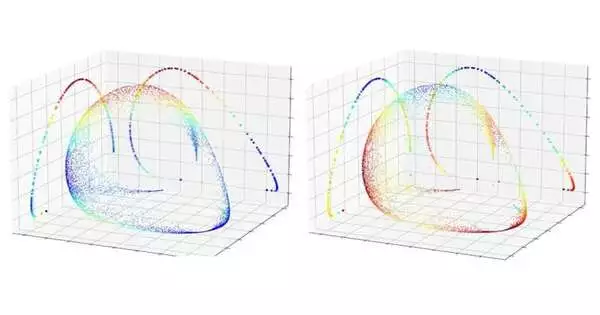
Rather than making a recreation that computes each and every variable in a given quantum framework, they tracked down an alternate methodology: subbing a bunch of numbers that depict the potential connections between each set of electrons. This is known as a “two-electron decreased thickness grid.”
“By estimating the set that depicts the two-electron decreased thickness grid, we wind up making a guide of the multitude of various stages the quantum framework can insight,” made sense of graduate understudy Sam Warren, the main creator of the review.
This “map” itself, he said, likewise offers valuable advantages: “It permits you to see changes that could somehow be missed, and it creates a truly strong perception that lets you effectively and immediately handle an undeniable level outline of the framework.”
The group had a go at utilizing the strategy to show a few various types of stage changes and found it was basically as exact as the customary, more serious technique.
“It gives us the key physical science we want to grasp the framework while limiting the figuring requests,” said graduate understudy LeeAnn Sager-Smith, the second creator on the review.
Mazziotti believes the strategy is helpful for running recreations on quantum PCs and for fostering how we might interpret quantum stage changes generally. “There are a few regions that have been underexplored on the grounds that they are so hard to show,” he said. “I trust this approach can open a few new entryways.”
More information: Samuel Warren et al, Quantum simulation of quantum phase transitions using the convex geometry of reduced density matrices, Physical Review A (2022). DOI: 10.1103/PhysRevA.106.012434