A customary paper crane is an accomplishment of creativity. Each crease in origami prompts the change of a solitary square piece of paper into a bird, a mythical beast, or a bloom. Origami deters sticking, checking or cutting the paper, yet in the craft of kirigami, decisively positioned cuts can change the state of the paper much further, making complex designs from basic cuts. A notable illustration of this is a spring up book, where contingent upon how the level paper is cut, an alternate arrangement of shapes — a heart, a frog, a bunch of high rises — will arise when the book is opened.
In assembling, kirigami is changing the round of what is conceivable. Very much like with paper, rehashed laser cutting of a sheet opens up the opportunities for complex shape-transforming fueled by the opening and shutting of cuts. Due to the opportunity accessible in planning cuts, this makes a wide selection of calculations that have profoundly versatile properties contrasted with customary materials. In true applications, you could see such a material utilized in mechanical technology or space, for example a snakeskin like kirigami-roused material that permits a robot to creep or a transforming airframe. Yet, before these materials can be adjusted for proficient use, we want to more readily comprehend how kirigami materials shape-shift under normal designing burdens and loads. While the standards for basic structure blocks are known, the principles for their aggregate shape-moving connections remain generally hazy.
In a new paper distributed in Physical Review Letters, a cross-disciplinary group of scientists at USC, University of Illinois at Chicago, and Stony Brook University determined another numerical condition for sorting the way of behaving of kirigami-roused materials to more readily foresee how they will move when pushed or pulled. The group incorporates USC Assistant Professor Paul Plucinsky and Post-doctoral Fellow Yue Zheng; Stony Brook University Assistant Professor Paolo Celli and Graduate Research Assistant Imtiar Niloy; and University of Illinois-Chicago Assistant Professor Ian Tobasco.
“These materials’ geometry is somewhat randomly controlled. As a result, we want guidelines for selecting the architectures that will be built. Once you have those rules, you must be able to model the system in order to make some reasonable predictions about how it will deform when pushed or pulled.”
Assistant Professor Paul Plucinsky
Said Plucinsky: “The math of these materials is tuned fairly randomly. So we want rules about how you could pick the models that you will create. When you have those standards, you likewise should have the option to show the framework so you make some sensible forecast of how it will twist when pushed or pulled.”
Plucinsky says past models of material way of behaving don’t matter to kirigami materials, as they are not delicate to the muddled math of their plans. “To have the option to utilize these materials, you need to see first why when you acquaint these examples with loads, they produce a non-uniform reaction.”
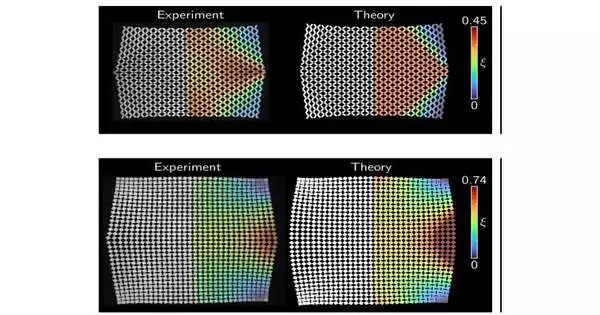
At the point when a material is cut, it produces “cells” or contained spaces that recurrent in an example, for example, parallelograms, Plucinsky said. On account of kirigami materials, these cells can be sorted to act in one of two ways: wave-like or rotting along curved circular segments, and this relies just upon whether the example packs or grows opposite to the pulling course. A numerical condition oversees the mathematical way of behaving of things like water stream, Plucinsky expressed, yet for solids like these, it is more earnestly to infer. A halfway differential condition (PDE) is what Plucinsky and his group had the option to create and go ahead as the main piece of a greater riddle expected to make kirigami materials basically relevant.
A displaying issue
At the present time, Plucinsky says while individuals are anxious to involve kirigami materials to plan gadgets in the delicate mechanical technology, biomedical, and even space research fields, there is an essential displaying issue that forestalls their utilization. Plucinsky said, there’s very little had some significant awareness of how kirigami materials capability under essential stacking conditions. “In the event that you don’t have a decent device to show the frameworks being referred to, you would struggle with exploring the plan space and making thorough forecasts about the singular examples,” Plucinsky said.
Considering that, Plucinsky and his exploration group thought, ‘is there a basic numerical condition that could portray these materials?” “The condition,” he said, “would permit you to foresee the way of behaving of the framework in a mathematically effective manner.”
The way in to the situation was to understand that kirigami cells, however having muddled building blocks themselves, could be conceptualized as iotas in a grid (a rehashing 2D arrangement of particles), like in a regular glasslike strong, where the units are indistinguishable and rehashing. From that point, it was easy to determine a condition that figured out how to mirror the progressions in the actual design of such a material when controlled. The condition gives knowledge into true situations, for example, how a kirigami-based space item could respond in the event that a moon rock arrived on it.
Unique pieces of plan
Kirigami designs, Plucinsky said, are useful for some reasons, one of which is they are material free in numerous ways. “This kind of equals pleasantly with added substance producing where they currently can essentially go in and at different scales make painstakingly designed designs. The fact is that the example matters, so assuming you plan the example accurately, the decision of material that you use doesn’t need to issue so a lot.”
Seeing the outcome of the numerical model in anticipating kirigami-roused materials makes the ways for involving such displaying for different materials, Plucinsky said. “We’re pursuing the possibility that assuming you have something with a rehashing design, you can find a condition that precisely models it. From that point, we can flip this completely around so that to design a specific property, you can say, ‘goodness, it necessities to include a x-type example,’ and figure out it.”
More information: Yue Zheng et al, Continuum Field Theory for the Deformations of Planar Kirigami, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.208003