Chiral zeroth Landau levels are single-direction, topologically protected bulk states. These levels are essential for breaking chiral symmetry and triggering the chiral anomaly, which involves the non-conservation of chiral currents in both particle physics and condensed matter systems in the fields of quantum field theory and condensed matter physics.
However, previous methods for achieving chiral Landau levels have relied on background magnetic fields and 3D Weyl degeneracies, both of which make sample fabrication difficult and restrict their application.
In a recent Light publication, A novel approach was presented by a group of scientists and Professor C. T. Chan from the Department of Physics at the Hong Kong University of Science and Technology in Hong Kong, China, in Science & Applications. They created a 2D Dirac cone photonic system with an inhomogeneous effective mass by displacing the local parity inversion symmetry that was present within each unit cell.
“We want to move the concept of chiral zeroth Landau levels from 3D Weyl systems to 2D Dirac cone systems. To accomplish this, we recognize that a 2D Dirac cone system can be regarded as a subsystem of a 3D Weyl system by introducing a virtual direction represented by the Dirac cone’s effective mass.”
This inhomogeneous successful mass made an engineered check field in a virtual course, which communicated with the Dirac decadence. They were able to experimentally validate the one-way propagative nature of the chiral Landau levels and successfully extend them from 3D to 2D systems as a result of their work.
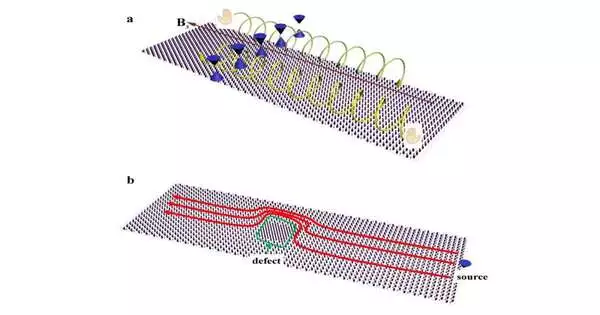
They also carried out experiments to test the chiral zeroth Landau levels’ resistance to backscattering and introduced flaws into the system. These findings hold the potential to be used in one-way optical design and significantly simplify sample fabrication.
Bulk states, in contrast to topologically protected surface states, are easier to use in communication devices. This is because edge states have energy that is primarily localized near the system’s boundary, making them more susceptible to leakage, whereas bulk states confine energy within the system. The underlying physics, exceptional properties, and potential applications of these bulk states were summarized by the researchers:
“From 3D Weyl systems to 2D Dirac cone systems, the idea of chiral zeroth Landau levels is our goal.” They stated, “We recognize that a virtual direction represented by the effective mass of the Dirac cone can be considered a subsystem of a 3D Weyl system in order to achieve this.”
“We can redefine the momentum in this virtual direction as a virtual canonical momentum by making the effective mass inhomogeneous.” Thus, this leads to an engineered attractive field on the 2D plane, which communicates with the Dirac cone and prompts the development of in-plane chiral Landau levels.”
“The scattering transition from a positively propagating zeroth mode to a negatively propagating mode is comparable to intervalley scattering due to the fact that a single Dirac cone supports only one chiral zeroth Landau level. Notwithstanding, this cycle poses critical difficulties because the two valleys are broadly isolated in energy space, making such changes truly challenging to happen,” they added.
“The chiral zeroth bulk mode’s exceptional properties are primarily due to its inherent robustness against defect-caused backscattering. Because of this, it is excellent for use in the design of one-way optical waveguides. It can be used in the optical frequency range by reducing the sample size from millimeters to nanometers. This opens up doors for its far-reaching use in specialized gadgets, successfully limiting energy spillage. According to the researchers, “the confined energy within the bulk enables efficient management of information transport, further improving its accessibility.”
More information: Hongwei Jia et al, Experimental realization of chiral Landau levels in two-dimensional Dirac cone systems with inhomogeneous effective mass, Light: Science & Applications (2023). DOI: 10.1038/s41377-023-01209-z