Geographical and trapping are two strong standards for describing the design of intricate quantum states. In another paper in the journal Physical Review X, scientists from the University of Pennsylvania lay out a connection between the two.
“Our work integrates two major thoughts,” says Charles Kane, the Christopher H. Browne Distinguished Professor of Physics in Penn’s School of Arts and Sciences. “It’s a calculated connection between geography, which is an approach to portraying the general elements that quantum states have, and trap, which is a manner by which quantum states can show non-nearby relationships, where something that occurs in one point in space is correlated with something that occurs in one more part of space.” What we’ve found is that what is going on where those ideas are firmly entwined. “
The seed for investigating this association came during the extended periods Kane spent in his work space during the pandemic, considering novel thoughts. One line of reasoning made them imagine the exemplary course book picture of the Fermi surface of copper, which addresses the metal’s potential electron energies. It’s an image each physics understudy sees, and one with which Kane was profoundly natural.
“Obviously, I found out about that image, harking back to the 1980s, yet I had never mulled over everything as depicting a topological surface,” Kane says.
“This might help us come up with fresh ideas for phases of matter that we don’t fully understand and don’t have as many tools to investigate.”
Charles Kane, Distinguished Professor of Physics in Penn’s School of Arts & Sciences
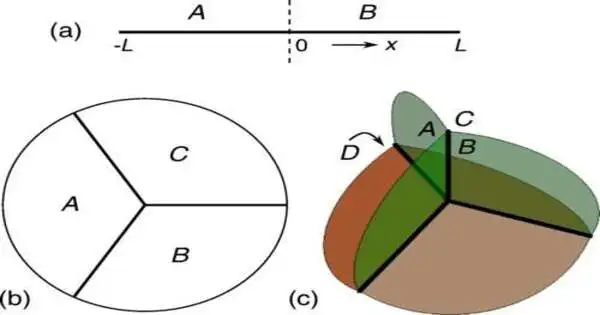
An exemplary perspective of topological surfaces, says Kane, is to think about the contrast between a doughnut and a circle. What’s the distinction? A solitary opening Geography considers these generalizable properties of a surface, which are not changed by twisting. Under this rule, an espresso mug and a doughnut would have a similar topological property.
Taking into account the Fermi surface of copper as a topological item, then, the related number of openings it has is four, a figure otherwise called a sort. When Kane started thinking about the Fermi surface along these lines, he puzzled over whether a relationship could exist between the sort and the quantum trap.
To additionally explore that likely association, Kane involved his alumni understudy, Pok Man Tam, and Martin Claassen, an associate teacher of material science at Penn who has zeroed in on quantum traps in his work. Together, they inferred a numerical connection between the sort of the Fermi surface and a proportion of the quantum trap called the common data. The shared data portrays the connections that can happen in unique locales of rooms that meet at a solitary point. The number known as the Euler trademark, which is firmly connected with the sort, gave the exact association between the two.
The scientists demonstrated that the connection between geography and trap was held in a basic metal framework, with electrons freely moving between each other, and then extended their investigation to demonstrate that the association was also present when electrons collaborated with greater complexity.
And keeping in mind that the hypothetical work was finished on metals, Kane accepts it will reach out to different materials too, for example, those that include solid connections between electrons.
“What this might permit us to do is devise better approaches for thinking about periods of issues that we don’t see quite well and don’t have as many instruments for investigating,” Kane says. Individuals are attempting to sort out some way to use quantum mechanics to exploit quantum data. That’s what to do. You need to comprehend how quantum mechanics shows itself when you have numerous levels of opportunity. That is a difficult issue, and this work is poking us along like that. “
In follow-up work, Kane and partners desire to configure tries to keep on investigating the newly discovered connection, maybe conceiving another method to gauge the topological sort and a method for testing the design of quantum traps.
More information: Pok Man Tam et al, Topological Multipartite Entanglement in a Fermi Liquid, Physical Review X (2022). DOI: 10.1103/PhysRevX.12.031022
Journal information: Physical Review X