Actual frameworks develop at a specific speed, which relies upon different elements, including the framework’s supposed topological design (i.e., spatial properties that are saved over the long run in spite of any actual changes that happen). Existing techniques for deciding the speed at which actual frameworks change over the long run, however, don’t represent these primary properties.
Two scientists at Keio College in Japan have as of late determined a speed limit for the development of actual states that likewise represents the topological design of a framework and of its basic elements. This speed limit, framed in a paper distributed in Actual Survey Letters, could have various important applications for the review and improvement of various actual frameworks, including quantum advances.
“Sorting out how quick a framework state can change is a focal point in old-style and quantum mechanics, which has drawn in the extraordinary interest of researchers,” Tan Van Vu and Keiji Saito, the scientists who did the review, told Phys.org. “Understanding the system of controlling time is pertinent to designing quick gadgets like quantum PCs.”
“Determining how quickly a system state can change is a crucial problem in classical and quantum mechanics that has piqued the interest of scientists.”
Tan Van Vu and Keiji Saito, the researchers who carried out the study,
The idea that there is a cutoff in the functional time expected for a framework to move starting with one actual state and then onto the next was first presented quite a few years ago by Leonid Isaakovich Mandelstam and Igor Tamm. From that point forward, other examination groups have investigated this thought further, finding comparable limits that can be applied to various sorts of physical science frameworks.
“These cutoff points, called “speed limits,” set extreme rates at which a framework can develop to a discernible state and have tracked down various applications,” Vu and Saito made sense of. “By and by, regular speed limits have the weakness of giving no significant limits as the size of the framework develops.” One of the clarifications is that the topological nature of the elements, which emerges from the organization design of basic elements, has not been as thoroughly considered as expected.
The vital goal of the new work by Vu and Saito was to devise another speed limit that likewise thinks about the topological design of an actual framework and its basic elements. This could at last assist with setting quantitatively rigid limits, possibly revealing the actual systemic changes starting with one state and moving onto the next. Simply put, none of the systems presented thus far are capable of accomplishing this.
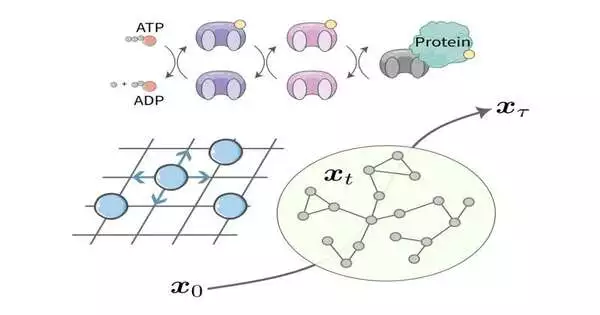
“Our thought is to utilize a summed-up form of the discrete Wasserstein distance to measure the distance between the states,” Vu and Saito said. “The Wasserstein distance starts from measuring the number of and how far a heap of products should be conveyed to make one more piece of merchandise from one knot.” This distance, broadly utilized in the ideal vehicle hypothesis, encodes topological data and can develop relative to the size of the framework.
To infer the bound-together topological speed limit, Vu and Saito planned the time advancement of actual states to the ideal vehicle issue, taking advantage of the properties of the ideal vehicle distance. As a feature of their review, they likewise demonstrated the legitimacy of their methodology by applying it to compound response organizations and connecting many-body quantum frameworks.
“As we would see it, the most eminent finding of our review is the disclosure of the topological speed limit, which yields exact expectations for functional times and can apply to many elements,” Vu and Saito said.
The new topological speed limit presented by this group of analysts could at last be applied to explore in different areas of material science, possibly working on the ongoing comprehension of various frameworks and at times working with their utilization for the advancement of new advances. For example, it empowers the making of a speed recipe for compound responses as well as setting general imperatives on the speed of bosonic transport and correspondence through turn frameworks.
“Later on, we intend to investigate further uses of the topological speed limit from different headings,” Vu and Saito added. “The use of as much as possible to more readily grasp the basic components of actual peculiarities, like the thermalization of closed and open frameworks, is a promising methodology.”
More information: Tan Van Vu et al, Topological Speed Limit, Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.130.010402
L. Mandelstam et al, The Uncertainty Relation Between Energy and Time in Non-relativistic Quantum Mechanics, Selected Papers (2011). DOI: 10.1007/978-3-642-74626-0_8