Turn glasses are combinations shaped by respectable metals in which a modest quantity of iron is broken down. There is no such thing as in spite of the fact that them in nature and have not many applications, they have by the by been the focal point of interest of measurable physicists for about 50 years. Investigations of twist glasses were pivotal for Giorgio Parisi’s 2021 Nobel Prize in Physical science.
The logical interest of twist glasses lies in the way that they are an illustration of a mind boggling framework whose components collaborate with one another in a manner that is in some cases helpful and in some cases ill-disposed. The math created to comprehend their way of behaving can be applied to issues emerging in different disciplines, from environment to AI, also financial aspects.
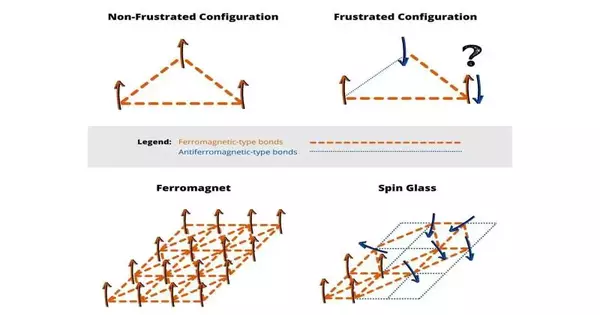
Turn glasses are attractive frameworks, that is to say, frameworks in which individual components, the twists, act like little magnets. Their quirk is the co-presence of ferromagnetic-type bonds, which will generally adjust the twists, with antiferromagnetic-type bonds, which will more often than not situate them in inverse headings.
“With the help of the mean-field theory, we can predict the exponents governing the transition above a so-called critical upper dimension. However, nobody knows for sure what this dimension is (5, 6, or a non-integer number?) or what occurs below it at this time.”
Carlo Lucibello, Assistant Professor in the Department of Computing Sciences
This makes lower-energy setups show remaining dissatisfaction: finding a plan of twists that fulfills all bonds is beyond the realm of possibilities. The baffled setups are likewise bunched in an immense (remarkable!) number of potential equilibria. This is as a glaring difference to what occurs in simply ferromagnetic frameworks, where at low temperature just two states are permissible (turn adjusted “up” or turn adjusted “down”).
To make a similarity with a biological system, having countless equilibria demonstrates a strong environment, ready to adapt, for instance, with the vanishing of an animal groups, through a set number of modifications. A low harmony number depicts a delicate framework, which requires various and convoluted revisions to get back to balance and can, hence, be truly harmed, in the event that not obliterated, by somewhat little bothers.
This phenomenology has been very much clarified and numerically portrayed in frameworks living in boundless aspect, purported mean-field frameworks, the answer for which was given by Parisi in 1979 and afterward better figured out in resulting a long time with the assistance of Marc Mézard (presently a full teacher at Bocconi) and Michelangelo Virasoro.
“Perhaps of the most discussed issue,” as Carlo Lucibello, Partner Teacher in the Branch of Figuring Sciences and co-creator, with Parisi and others, of a paper just distributed in Actual Survey Letters makes sense of, “is how much mean-field phenomenology applies in low dimensionality.”
For we realize that in aspect 1, that is to say, on one twist chain, the framework is consistently in a paramagnetic stage, so by bringing down the temperature there are no changes either to a twist glass stage with its numerous equilibria or to a straightforward ferromagnetic stage.
“There is a supposed basic upper aspect,” Lucibello says, “above which the mean-field hypothesis applies, permitting us to foresee the types overseeing the progress. Right now, in any case, nobody can say without a doubt what this aspect is (5, 6, or a non number?) and what occurs underneath it.”
The paper just distributed by Lucibello and co-creators presents another numerical method for examining limited layered frameworks. The new hypothesis predicts a basic higher element of 8, so we can sensibly presume that twist glasses in our three-layered world are probably not going to be portrayed by a mean-field hypothesis and that there is still a great deal of work to do in this part of hypothetical physical science.
More information: Maria Chiara Angelini et al, Unexpected Upper Critical Dimension for Spin Glass Models in a Field Predicted by the Loop Expansion around the Bethe Solution at Zero Temperature, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.075702
Journal information: Physical Review Letters