In the diary Actual Survey Letters, a group of specialists from the College of Twente depict how any sort of wave, whether quantum or traditional, is restricted in any sort of precious stone. The outcomes will outstandingly support productive new coordinated circuits that steer data encoded in minuscule light heartbeats through shrewd urban areas.
Waves are an inseparable part of our daily lives, whether we are standing by listening to music, looking in the mirror, or experiencing the sea shaking on a cruising transport.A focal point in controlling waves for applications requires the capacity to limit the waves in little locales in space.
Researchers definitely realize that it’s conceivable by intentionally presenting custom-fit deviations from ideal periodicity into the gem. Yet, how precisely are the waves secured? Is it safe to say that they are bound in all aspects all the while, or do they hold the opportunity to move along a line or in a plane? Astoundingly, the vital stage from having the gem’s design to anticipating the control of waves had not been taken up to this point.
You may know about precious stones shaped by minerals in nature. Such gems can be utilized to bind quantum-mechanical electronic waves. The man-caused precious stones of silicon have prompted the revelation of electronic semiconductors, the reason for the continuous advanced upset. We presently realize that there are different kinds of precious stones that can limit and control various sorts of waves, like light, sound, and possibly even tremors.
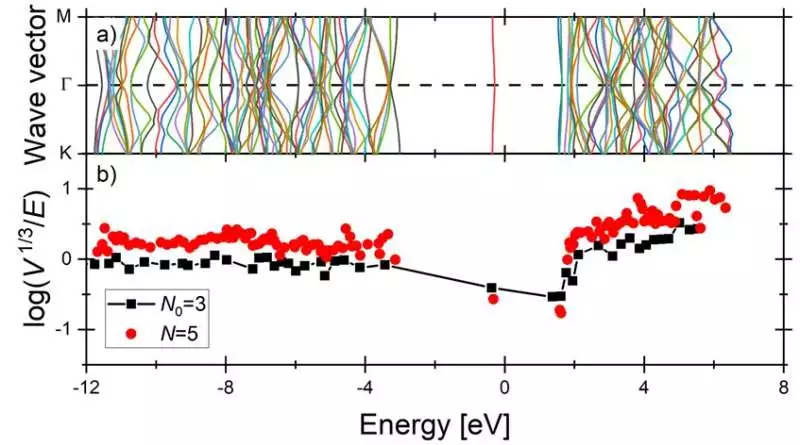
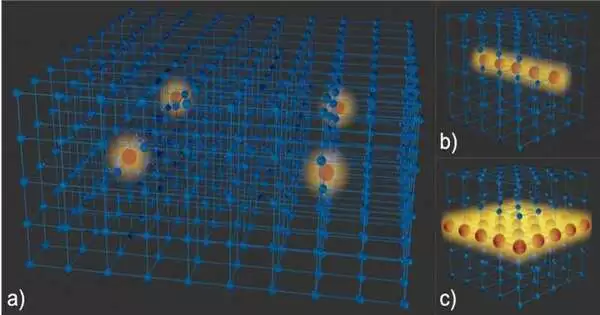
Figure 2: Constraint examination of a 2-layered quantum precious stone for electrons in the semiconductor hexagonal boron-nitride with a nitrogen opportunity (a) Precious stone scattering relationships(b) Registered proportion of the constraint volume to control energy for each spreading band of wavesRed focuses are compared to groups in the gem with size N = 5, while dark focuses are compared to groups in the gem with size N = 3.With the expanded size, groups with c = 2 imprisonment drop down and groups with c = 0 climb in the diagram and are consequently obviously recognized. Because of the wave imprisonment calculation, it turns out there are no c=1 groups. Twente University of Technology
Having a current gem isn’t sufficient to bind waves. The interior construction of the precious stone must explicitly suit the ideal application. To make matters more confounded, there are endless opportunities for this construction, taking into account all possible structure blocks and their game plans in the gem. Until now, researchers and specialists attempting to limit waves had to rely on intuition, mystery, and costly experimentation tests.
In their Actual Survey Letters paper, the Twente scientists present a strong examination device that predicts how waves are kept from a gem, involving just the gem’s construction as info. First creator and Ph.D. understudy Marek Kozon MSc makes sense of, “A focal boundary in our examination is a ‘control dimensionality’ that we have concocted. It depicts the constraints for every possible wave.”
COPS bunch pioneers Prof. Dr. Willem Vos and Prof. Dr. Promotion Lagendijk add eagerly: “We got energized when we understood from conversations with Marek that our technique relates not exclusively to traditional waves like sound and light but additionally to quantum waves, for example, electrons in small nanostructures.”
In light of the new skill, the fashioners of precious stones can now profit from new “general guidelines” for explicit applications, bringing about profoundly rearranged and consequently productive planning processes. Dr. Matthias Schlottbom and Prof. Dr. Jaap van der Vegt add: “Our outcomes are significant for proficient data handling in new photonic and electronic chips that will populate future brilliant urban communities.”
More information: Marek Kozoň et al, Scaling Theory of Wave Confinement in Classical and Quantum Periodic Systems, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.129.176401
Journal information: Physical Review Letters