AI (ML) is for the most part characterized as information-driven innovation emulating shrewd human capacities, which step by step overhauls its exactness as a matter of fact. It begins with gathering gigantic amounts of information, like numbers, texts, pictures, etc. In the wake of preparing the information, ML calculations fabricate a coherent model to distinguish designs through the most unimaginable human mediation. With the assistance of test-preparing information, software engineers test the model’s legitimacy prior to presenting a new dataset. The better the forecast, the more preparation information there is.
Nonetheless, we can’t anticipate solid examples or expectations for new information if the preparation dataset is one-sided, conflicting, or even off-base. In any case, with the quick development of this field, we can oblige ML models by upholding a physical science structure that reliably submits to normal regulations.
In our new work in Diary of Applied Physical Science, we have created one such truly compelled ML model to acquire knowledge into the electrostatics of a metal-oxide-semiconductor (MOS) capacitor, which is the major structure block of present CMOS (correlative metal-oxide-semiconductor) innovation.
A MOS capacitor consists of a doped semiconductor body, a slender separator (i.e., oxide), and a metal terminal called the door. Contingent on the value of the applied entryway voltage, it works in three modes: amassing, consumption, and reversal. In the gathering mode, versatile charge transporters like the dopant type structure a dainty layer by collecting at the oxide-semiconductor interface.
With expanding door voltage, the connection point progressively becomes drained of versatile charges, abandoning fixed particles of the opposite extremity. It leads to an extended possible drop at the semiconductor surface. With additional heightening in entryway voltage, a layer of versatile charge transporters of reversed dopant type yet with comparative focus structures lies underneath the oxide-semiconductor interface. Subsequently, we say the MOS capacitor has gone into reversal mode.
The electrostatics of a MOS capacitor are represented by the Poisson-Boltzmann condition (PBE), which is an exceptionally nonlinear differential condition (DE). A DE addresses the interrelationship between a component of at least one free factor and its subsidiaries. The capability implies an actual amount, and the subordinate demonstrates the pace of progress for the free factors.
Setting up nonlinear DEs on a PC is best since scientific arrangements are typically interesting. Standard strategies (e.g., limited contrast strategy, limited component technique, shooting strategies, splines) and easy-to-understand programming bundles based on these methods are accessible for settling different DEs.
Brain organizations (NNs), a subset of ML that has arisen in the past with critical effects in a few science and design disciplines, can settle nonlinear DEs easily. They utilize interconnected hubs in a layered construction looking like the human cerebrum, which makes organic neurons sign to each other.
NNs can precisely estimate confounded multivariate capabilities and manage hardships in traditional procedures, e.g., reliance on discretization in limited component techniques and splines. The essential disadvantage of NNs is that their preparation is slow and computationally debilitating. Notwithstanding, we have beaten this test with upgrades in processing and streamlining methods. Here, we research whether a machine can get familiar with the actual rule of a MOS capacitor by settling the PBE using ML.
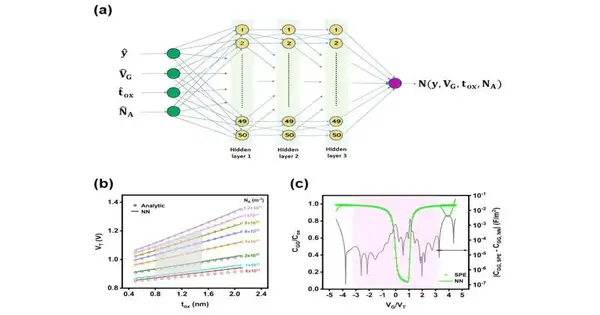
A feedforward brain network was utilized for developing the preliminary arrangement of the Poisson-Boltzmann condition. (b) Variety of a limit voltage as a component of various doping focuses (c) Model extrapolation of standardized entryway capacitance on the scale; the concealed area addresses the inspecting space. Credit: Creators
A methodology called PINN (physical science-informed brain organization) has proactively become exceptionally well known for tackling DEs emerging from the actual sciences (Burger condition, Schrodinger condition, and so on). However, it is really flexible and can be utilized to handle any DE; the limit conditions (BCs) are not hard-compelled in PINN.
Rather, alongside the DE, they are joined as a punishment into a misfortune capability, which registers the contrast among anticipated and genuine qualities in the ML model. Subsequently, it doesn’t ensure to precisely fulfill the BCs. Then again, Lagaris et al. have proposed one more method to bypass this issue.
It utilizes the overseeing condition to find a preliminary arrangement that appropriately fits the DE. This approach precisely fulfills the BCs. Be that as it may, there is no broad system to develop such preliminary arrangements, particularly for the mind-boggling limit conditions we face on account of a MOS capacitor.
Our way to deal with addressing PBE for MOS capacitors is outlined by PINN, and the strategy for Lagaris et al. As of not long ago, the last technique has been utilized to produce preliminaries for Neumann and Dirichlet BCs, which is generally clear. In examination, our PBE requires both basic Dirichlet BC and complex Robin BC, including a capability and its derivate.
Regardless of its profoundly nonlinear nature, we showed that it is testing yet conceivable to utilize the strategy for Lagaris et al. to fabricate preliminary arrangements in a practical structure (i.e., a capability that accepts at least one capability as contention) that fulfills both BCs of the PBE. In our model, we have exactly tested the actual area of the gadget to develop the misfortune capability from the preliminary arrangement.
The quantity of tests determines the intricacy of figuring out the misfortune capability and advancing the preliminaries. Hence, we have considered a material science-based inspection plan and brought gadget boundaries stochastically into the model. This approach has helped the model achieve extraordinary precision.
We have approved our model against customary mathematical techniques accessible in Python, as well as the business standard surface possible condition (SPE).
Through this review, we have found that our NN model can gain proficiency with the connection between input factors (i.e., thickness of the semiconductor, entryway voltage, oxide thickness, and doping fixation) and the semiconductor potential.
Also, it can catch a few significant parts of MOS gadget physical science, like the doping-subordinate consumption width, variety of limit voltage with oxide thickness and doping, and low-recurrence capacitance-voltage qualities, as well as deciphering the collection, exhaustion, and reversal systems. This model keeps on submitting to gadget material science, even outside the testing area.
In outline, interestingly, we report the chance of a ML model to duplicate the principal material science of MOS capacitors without utilizing any named information (as opposed to ordinary directed ML). We show that the generally utilized PINN approach neglects to gain proficiency with the Poisson-Boltzmann condition because of the dynamic nature presented by the extraordinary limit conditions.
We figure out a parametric model that normally fulfills the limit conditions, so the expressive force of brain organizations can be bridled to protect arrangements with remarkable precision. Furthermore, we demonstrate the way that the proposed model can precisely catch basic bits of knowledge, for example, exhaustion width, limit voltage, reversal charge, and so on.
This story is important for Science X Exchange, where scientists can report discoveries from their distributed exploration articles. Visit this page for data about ScienceX Discourse and how to take part.
More information: Tejas Govind Indani et al, Physically constrained learning of MOS capacitor electrostatics, Journal of Applied Physics (2023). DOI: 10.1063/5.0168104





