In the recent concern of Nature Photonics, Prof. Dr. Oliver G. Schmidt, Dr. Libo Mama, and accomplices present a methodology for noticing and controlling the optical Berry ease in Möbius ring microcavities. In their exploration paper, they examine how an optical Berry stage can be created and estimated in dielectric Möbius rings. Furthermore, they present the primary trial evidence for the presence of a variable Berry stage for enraptured resounding light that is either directly or circularly enraptured.
A Möbius strip is an entrancing item. You can easily make a Möbius strip by curving the two ends of a piece of paper by 180 degrees and interfacing them together.After looking into it further, you understand that this strip has just a single surface that can’t be recognized inside and outside, underneath, or more. Due to this extraordinary topological property, the Möbius strip has turned into an object of endless numerical discussion, creative portrayals, and reasonable applications, for instance in canvases by M.C. Escher, as a wedding band, or as a drive belt to similarly wear the two sides of the belt.
Optical ring resonators
Shut groups or rings likewise assume a significant role in optics and optoelectronics. Up to this point, be that as it may, they have not consisted of Möbius strips and they are not made of paper, yet they are made of optical materials, for instance, silicon and silicon dioxide or polymers. These “typical” rings are likewise not centimeters in size but rather micrometers. In the event that light with a specific frequency propagates in a miniature ring, helpful obstructions make optical resonances happen. This standard can be exemplified by a guitar string, which produces various tones at various lengths. The more limited the string, the more limited the frequency, and the higher the tone.
An optical reverberation or valuable impedance happens precisely when the outline of the ring is different from the frequency of the light. In these cases, the light resounds in the ring, which is called an optical ring resonator. Interestingly, the light is emphatically lessened, and disastrous impedance happens when the perimeter of the ring is an odd number for a portion of the frequency of the light. Consequently, an optical ring resonator upgrades light of specific frequencies and emphatically weakens light of different frequencies that don’t “fit” in the ring. In mechanical terms, the ring resonator goes about as an optical channel that, coordinated on a photonic chip, can specifically “sort” and cycle light. Optical ring resonators are focal components of optical sign handling in present-day information correspondence organizations.
How energized light moves through the Möbius strip
Polarization, like frequency, is a fundamental property of light.Light can be energized in different ways, for instance, straightly or circularly. Assuming light spreads in an optical ring resonator, the polarization of the light doesn’t change and continues as before at each point in the ring.
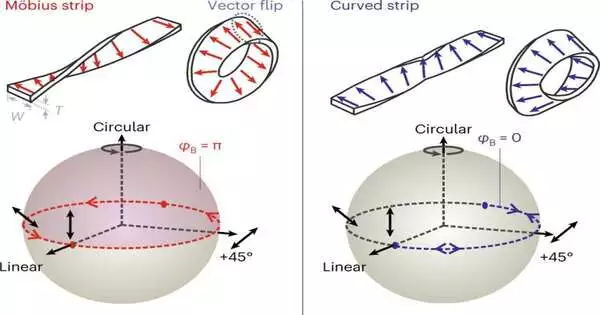
The circumstance changes essentially in the event that the optical ring resonator is supplanted by a Möbius strip, or better, a Möbius ring. To more readily comprehend this case, it helps to consider the details of the calculation of the Möbius ring. The cross-part of a Möbius ring is regularly a slim square shape in which two edges are significantly longer than their two nearby edges, like in a meager piece of paper.
Allow us to anticipate straight, energized light paths in the Möbius ring.Since the polarization likes to adjust itself toward the long cross-sectional side of the Möbius ring, the polarization ceaselessly turns up to 180 degrees while passing totally around the Möbius ring. This is a significant difference from a “normal” ring resonator, in which the polarization of the light is constantly maintained.
Furthermore, that is not all. The turning of the polarization causes an adjustment of the period of the light wave, so the optical resonances never again happen at full frequency products that fit into the ring, but at odd products of a portion of the frequency. In 2013, a member of the exploration team predicted this impact hypothetically.This expectation, therefore, depends on the work of physicist Michael Berry, who presented the eponymous “Berry stage” in 1983, depicting the adjustment of the period of light whose polarization changes as it engenders.
First experimental evidence
In the ongoing article distributed in the journal Nature Photonics, the Berry period of light circling in a Möbius ring is tentatively uncovered in an interesting way. For this reason, two rings with a similar breadth were made. The first is a “typical” ring, and the second is a Möbius ring. Furthermore, as anticipated, the optical resonances in the Möbius ring show up at various frequencies compared with the “typical” ring.
The exploratory outcomes, in any case, go a lot beyond past forecasts. For example, direct polarization turns, but it also becomes increasingly circular.The resonances do not occur at odd products of a portion of the frequency, but rather at non-whole number products.To figure out the justification behind this deviation, Möbius rings with diminishing strip width were made. This study uncovered that the level of ellipticity in the polarization and the deviation of the reverberation frequency compared with the “typical” ring turned out to be continuously more fragile as the Möbius strip became smaller and smaller.
This can be effectively perceived on the grounds that the exceptional topological properties of the Möbius ring converge into the properties of an “ordinary” ring when the width of the band diminishes to that of its thickness. However, this also implies that Berry’s deliberate work in Möbius rings can be effectively limited by simply changing the design of the band.
Aside from the intriguing new central properties of optical Möbius rings, new mechanical applications are also emerging. Tunable optical berries that work in Möbius rings could be used for all-optical information handling of traditional pieces as well as qubits, as well as to support quantum rationale doors in quantum calculation and recreation.
More information: Jiawei Wang et al, Experimental observation of Berry phases in optical Möbius-strip microcavities, Nature Photonics (2022). DOI: 10.1038/s41566-022-01107-7
Journal information: Nature Photonics