The early outcome of material science comes mostly from taking care of immediate or forward issues in which the actual condition of a framework can be portrayed from an obvious actual model and from overseeing conditions. However, there exists an alternate sort of issue—backwards issues—that is trickier to tackle yet is significant to fields like design, astronomy, and geophysics.
To solve these inverse problems, you need to take a set of observational data and reverse the problem, or work backwards, to find the factors that caused the data to be there.
Gilberto Corso and Joo Medeiros de Araujo, researchers at the Universidade Federal do Rio, recently published a paper in The European Physical Journal B that looks into the possibility of using statistical data from noise statistics to solve inverse physics problems.
“As a rule, actual issues can be seen as immediate or reverse issues.” We try to find the solution in the direct case because we know the model’s parameters,” Corso stated. In the opposite case, we know the experimental arrangement, and we attempt to find the model that has produced such an answer.”
“In general, physical problems can be classified as direct or inverse. In the direct example, we know the model’s parameters and try to find a solution. In the inverse instance, we know the empirical solution and strive to determine the model that produced it.”
Universidade Federal do Rio researchers Gilberto Corso
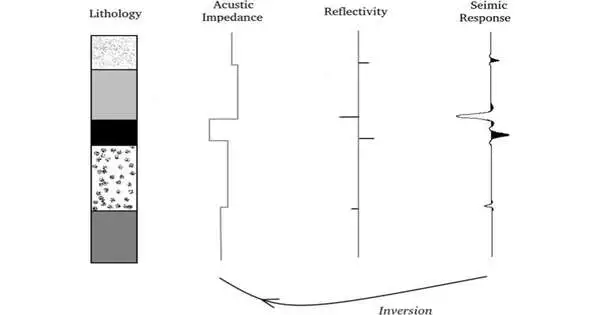
To survey backwards issues, the creators applied the utilization of Tsallis measurements, an assortment of numerical capabilities, and related likelihood circulations to a seismic reflection issue that is run of the mill in the oil business. In this scenario, waves are created on Earth’s surface, reflect in geologic strata, and are then recorded when they return to the surface.
This data is used to build a model of Earth’s subsurface, which is an inverse problem. However, when the wave data gets to the surface, it is tainted with useless information, or “noise.” The group wanted to know if this noise could actually make an inversion better.
Corso explained, “The noise is the main problem with inverse problems.” Tsallis statistics, for instance, can be used to model a variety of natural noises. Additionally, the commotion data could be utilized to improve the reversal.”
Making a reproduction of a complicated framework contaminated with clamor, the researchers found that backwards issues couldn’t be settled with the utilization of Tsallis commotion. This was something that Corso said was surprising. The scientists added that he and his coworker now plan to investigate other kinds of noise to see if they are just as bad at making an inversion go up.
“We mean to investigate in more detail different sorts of commotion circulations to examine our theory and other clamor models,” Corso finished up.
More information: Adson Alexandre Quirino da Silveira et al, Puzzle in inverse problems: Tsallis noise and Tsallis norm, The European Physical Journal B (2023). DOI: 10.1140/epjb/s10051-023-00496-0