How much pressure do pipes go through when a fluid courses through them, and how can it depend upon the level of ebb and flow of the line?
Twists in pipes are particularly vital, for instance, in the aortic curve that is associated with the left ventricle of the human heart. Channeling frameworks in modern plants frequently incorporate twists of 90 degrees or more, can be helical, and might have 180-degree twists. Liquid mechanists in Sweden have broken down liquid streams in such lines with a 180-degree twist. Their exploration is distributed in the diary Actual Audit Liquids.
Twists in pipes are not quite the same as their straight segments on the grounds that, in the bended areas, there are outward divergent powers because of the idleness of the fluid inside. That power is adjusted by a tension slope from the external mass of the line to the inward wall. Since the liquid speeds in a fanciful cut through the line won’t be equivalent in the bended segment—for instance, the speed close to the external mass of the line will be more noteworthy than close to the inward wall—an optional stream design, other than the movement through the line, is set up opposite to the principal stream course.
“Our research helps us understand where a sudden transition in the normally laminar aortic arch might occur. Indeed, the turbulent regime in the aorta may be linked to a variety of heart diseases.”
Said Massaro, the co-author of the study and a graduate student in the department of Engineering Mechanics at the KTH Royal Institute of Technology in Stockholm.
This movement is a couple of counterrotating, symmetric vortices, called senior member vortices, after the English researcher William Reginald Dignitary, which show up in the main twist in the line and can muddle the stream later for both laminar and tempestuous streams.
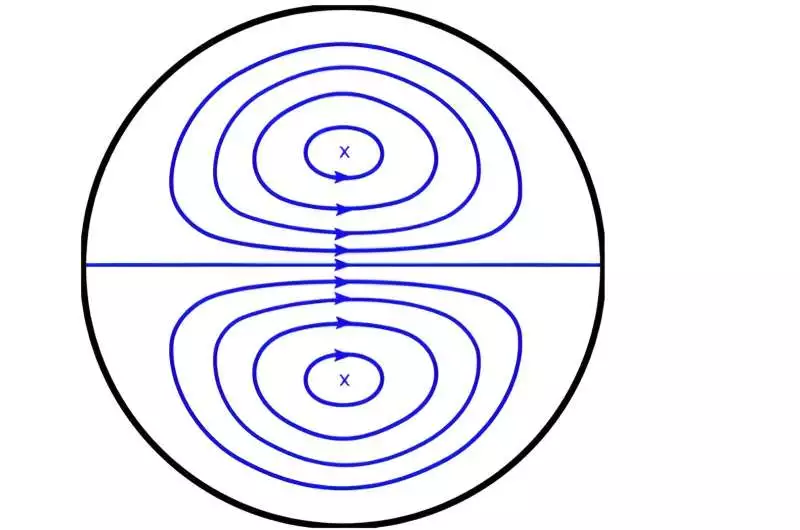
Dignitary vortices in a cross-section of a line. Credit: Rudolf Hellmuth, CC Attribution-Offer The same 4.0 Global, en.wikipedia.org/wiki/File:DeanVortices.svg
For a solitary twist, the inside math of the stream can be depicted by the Dignitary number, which relies upon the span of the line relative to how much ebb and flow there is in the curve, and the liquid’s Reynolds number, which is the proportion of inertial powers to gooey powers inside a liquid. Liquids have a basic Reynolds number that portrays their change from a smooth, laminar stream to a tempestuous stream, and this can be twice as extensive as in a straight stream. (As a matter of fact, a violent stream from a straight line can get back to laminar after entering a twisting part of the line.)
Generally, Reynolds numbers under 2,000 show a laminar stream; those over 3,500 show a violent stream, with progress from laminar to a tempestuous stream happening somewhere in the middle. The senior member number estimates the force of the inward auxiliary stream.

Change from laminar to tempestuous stream in a candle fire. Credit: Gary Settles, CC BY-SA 3.0, commons.wikimedia.org/w/index.php?curid=29522249
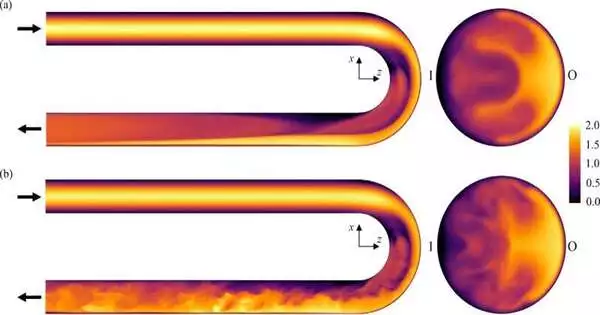
Daniele Massaro and partners at the KTH Regal Establishment of Innovation in Stockholm utilized a refined technique to mathematically and computationally settle the broadly muddled Navier-Stirs up liquid conditions to examine the change (from laminar to fierce stream) in a glorified line with a twist of 180 degrees, contrasting their finding with prior results for elbow (90 degree twist) and toroidal lines.
Expecting a delegated pipe ebb and flow of 1/3—the proportion of the sweep of a cross-segment of the line and the range of shape—the gathering isolated the reenacted liquid into around 30 million frameworks, not all uniform. They then, at that point, tackled the conditions for the lattice focuses as they changed with time.
By playing out a solidity examination—deciding the development of little, minuscule blemishes that show up in the underlying smooth liquid—the estimation decides the progressions in the liquid as it adjusts the twist. The progressions happen through every one of the upward cross-areas of the liquid and along the length of the line. Along these lines, the progress of the stream from laminar to tempestuous is not set in stone.
The extraordinary estimation—for which supercomputers were required, Massaro said, with runs that could require months—found the basic Reynolds number for the change to be 2,528. This is the district of the Reynolds number of the liquid, paying little heed to type, where unsteadiness emerges and the state of the design prompts the progression to disturbance. This change point is otherwise called a “Hopf bifurcation.” The unsteadiness of the 180-degree twist grows similar to that of a 90-degree twist. The basic Reynolds number for a 90-degree twist is 2,531, and for a torus, it is 3,290.
Because of the definite idea of shakiness, pipes with twists more noteworthy than 180 degrees are supposed to be comparable, but to a limited extent. For pipes with more limited twists, the Hopf bifurcation should vanish as the point of the curve approaches zero, with the stream staying laminar. The gathering gauges indicate that the bifurcation evaporates at a curve of around 20 degrees.
Albeit the examination has clear modern applications, the expansion to the heart isn’t directly a result of the contrast between genuine blood and this study’s romanticized stream. “Our review comprehends where an unexpected change in the, typically, laminar aortic curve could happen,” said Massaro, the co-creator of the review and an alumni understudy in the branch of Designing Mechanics at the KTH Imperial Foundation of Innovation in Stockholm. “To be sure, the tempestuous system in the aorta might possibly be connected with different heart illnesses.”
More information: Daniele Massaro et al. Global stability of 180∘-bend pipe flow with mesh adaptivity, Physical Review Fluids (2023). DOI: 10.1103/PhysRevFluids.8.113903