Perhaps the purest type of mathematics is number theory, which focuses on the properties of positive integers. It might appear to be far too abstract to be applicable to the natural world at first glance. Truth be told, the persuasive American number scholar Leonard Dickson expressed, “Say thanks to God that the number hypothesis is stainless by any application.”
But, over and over, the number hypothesis tracks down surprising applications in science and design, from leaf points that (nearly) all around follow the Fibonacci succession to present-day encryption procedures in light of figuring indivisible numbers. Presently, specialists have shown a surprising connection between the number hypothesis and transformative hereditary qualities. The Journal of The Royal Society Interface contains their work.
In particular, the group of researchers—who hail from Oxford, Harvard, Cambridge, GUST, MIT, Imperial, and the Alan Turing Institute—found a strong connection between the sums-of-digits function from number theory and the phenotype mutational robustness, which is a crucial genetic quantity. The average probability that a point mutation will not alter a phenotype—a characteristic of an organism—is the definition of this quality.
“We’ve known for a long time that many biological systems have remarkably high phenotype robustness, which is essential for evolution. But we didn’t know what the exact maximum robustness imaginable was, or if there was one at all.”
Professor Ard Louis from the University of Oxford, who led the study,
The revelation might have significant ramifications for transformative hereditary qualities. Numerous hereditary changes are impartial, implying that they can gradually aggregate after some time without influencing the feasibility of the aggregate. Over time, these neutral mutations lead to a steady change in the genome sequence. Since this rate is known, researchers can look at the rate distinction in the arrangement between two life forms and determine when their most recent normal precursor lived.
Be that as it may, the presence of these unbiased transformations suggested a significant conversation starter: what part of transformations to a succession are unbiased? The average number of mutations that can occur across all sequences without affecting the phenotype is referred to as phenotype mutational robustness.
“We have known for some time that many biological systems exhibit remarkably high phenotype robustness, without which evolution would not be possible,” stated the study’s lead author, Oxford University Professor Ard Louis. However, we lacked knowledge of the absolute maximum robustness that could be achieved, if any.”
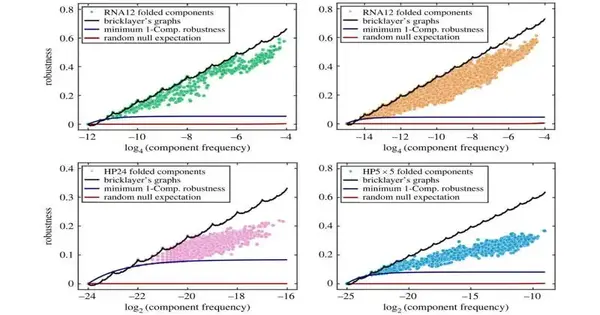
It is definitively this question to which the group has replied. They demonstrated that the greatest vigor is relative to the logarithm of the small portion of all potential groupings that guide to an aggregate, with a revision given by the amounts of digit capability sk(n), characterized as the amount of the digits of a characteristic number n in base k. For instance, for n = 123 in base 10, the digit total would be s10(123) = 1 + 2 + 3 = 6.
The fact that the maximum robustness also turns out to be related to the well-known Tagaki function, an odd function that is continuous everywhere but distinguishable nowhere, was another surprise. Due to its resemblance to the French dessert, this fractal function is also referred to as the blancmange curve.
First creator Dr. Vaibhav Mohanty (Harvard Clinical School) added, It is most astounding that we found obvious proof in the planning from groupings to RNA optional designs that nature at times accomplishes the specific greatest vigor bound. Maybe science realizes the fractal amounts of digits capability.”
“The beauty of number theory lies not only in the abstract relationships it uncovers between integers but also in the deep mathematical structures it illuminates in our natural world,” added Professor Ard Louis. We accept that many charming new connections between the number hypothesis and hereditary qualities will be seen from now on.”
More information: Vaibhav Mohanty et al, Maximum mutational robustness in genotype–phenotype maps follows a self-similar blancmange-like curve, Journal of The Royal Society Interface (2023). DOI: 10.1098/rsif.2023.0169