Mathematics

In fields like physical science and design, fractional differential conditions (PDEs) are utilized to show complex actual cycles to produce an understanding of how the absolute most convoluted physical and normal frameworks on the planet are capable. To address these troublesome conditions, analysts utilize high-constancy mathematical solvers, which can be extremely tedious and computationally costly to run. The ongoing work on other options, information-driven substitute models, figures out the objective property of an answer for PDEs as opposed to the entire arrangement. Those are prepared on a bunch of information that has been produced by the high-loyalty solver to foresee

Recently distributed research rethinks the assessment of logical discoveries, proposing an organization-based philosophy for contextualizing a distribution's effect. This new strategy, which is spread out in an article co-written by Alex Doors, an associate teacher with the College of Virginia's School of Information Science, will permit mainstream researchers to all the more decently measure the effect of interdisciplinary logical revelations across various fields and time spans. The discoveries are distributed in the diary procedures of the Public Foundation of Sciences. The effect of a logical distribution has, for some time, been measured by a reference count. Nonetheless, this approach is

Math specialists have developed better approaches to give additional proof to human-caused worldwide warming and foresee how close Earth is to arriving at risky environmental tipping points. Tipping points happen when bunches of little changes in the environment develop to make an unexpected, enormous change. Passing these limits prompts sped up warming and outrageous climate events. For instance, in years to come, the Atlantic Meridional Upsetting Flow (AMOC) is in danger of imploding. The AMOC is a sea momentum transport framework that carries warm water toward the North Atlantic and assists with managing temperatures in Europe and North America. Assuming

Perhaps the purest type of mathematics is number theory, which focuses on the properties of positive integers. It might appear to be far too abstract to be applicable to the natural world at first glance. Truth be told, the persuasive American number scholar Leonard Dickson expressed, "Say thanks to God that the number hypothesis is stainless by any application." But, over and over, the number hypothesis tracks down surprising applications in science and design, from leaf points that (nearly) all around follow the Fibonacci succession to present-day encryption procedures in light of figuring indivisible numbers. Presently, specialists have shown a

With the so-called ninth Dedekind number, researchers at Paderborn University and KU Leuven have solved a decades-old mathematical mystery, making history with 42 digits. Since 1991, experts all over the world have been looking for its value. With the help of the Paderborn-based Noctua supercomputer, the scientists were able to determine the exact numbers in the order that they appeared. At the International Workshop on Boolean Functions and Their Applications (BFA) in Norway in September, the findings will be presented. Lennart Van Hirtum, who was a computer science student at KU Leuven at the time and is now a research

Specialists at the College of Tsukuba have developed another technique for inferring straight conditions from convoluted nonlinear issues. Utilizing recreation results, they show that the model determined utilizing their proposed pseudo-linearization approach yields reactions that are closer to those of the notable elective strategy. This work can assist researchers and architects in anticipating and applying criticism to mechanical frameworks depicted with nonlinear conditions. The paper is distributed in the journal Logical Reports. Mathematicians frequently separate conditions into classifications, relying on the fact that they are too muddled to address. Direct conditions, in which factors would show up as a straight

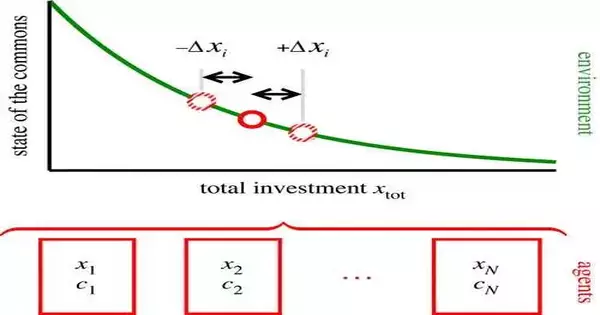
Without guidelines for their utilization, the state of openly available assets, for example, fish stocks, water, or air, can crumble emphatically. In financial matters, this is alluded to as the "awfulness of the hall." Elinor Ostrom became the first woman to receive the Nobel Prize in Economic Sciences in 2009 for her research on this topic. Ostrom's inquiry of how to forestall this "misfortune" is similarly pertinent today as it was nearly a while ago. The game hypothesis manages circumstances in which various specialists rival one another, with every member attempting to separately expand their own benefit. One discusses "Nash