By means of huge reenactments on supercomputers, an examination group from the Department of Physics, the University of Hong Kong (HKU), found obvious proof to portray an exceptionally caught quantum matter stage — the quantum turn fluid (QSL), a period of issue that stays confused even at extremely low temperatures. This examination has as of late been distributed in npj Quantum Materials.
P. W. Anderson, the Nobel Physics Laureate of 1977, proposed QSLs in 1973. They can possibly be utilized in topological quantum processing and to assist with understanding the systems of high-temperature superconductors that could extraordinarily reduce energy costs during power transport due to the shortfall of electrical opposition.
The QSL is known as a “fluid” because of its absence of regular requests. QSLs have a topological request that begins with long-range areas of strength and ensnarement. The discovery of this topological request is an intense undertaking because of the absence of materials that can impeccably accomplish the many model frameworks that researchers propose to track down a topological request of QSL and demonstrate its presence. In this way, there has not been solidly acknowledged substantial proof that QSLs exist in nature.
“In our work, we simulate a very complex model that is supposed to have topological order using the better processing capacity of contemporary supercomputers. Our discoveries have increased physicists’ confidence that QSLs should exist in nature.”
Jiarui Zhao, the first author of the journal paper and a Ph.D. student at the Department of Physics.
By means of a painstakingly planned mathematical trial on supercomputers, Jiarui Zhao, Dr. Receptacle Bin Chen, Dr. Zheng Yan, and Dr. Zi Yang Meng from the HKU Department of Physics effectively examined this topological request in a period of the Kagome grid quantum turn model, which is a two-layered cross section model with natural quantum snare and proposed by researchers that have Z2 (a cyclic gathering of request 2) topological request, by means of a painstakingly planned mathematical trial on supercomputers Their unambiguous consequences of topological trap entropy firmly recommend the presence of QSLs in high ensnarement quantum models from a mathematical point of view.
“Our work exploits the prevalent registering force of current supercomputers, and we use them to reproduce an exceptionally convoluted model which is known to have topological request.” With our discoveries, physicists are more certain that QSLs ought to exist in nature, “said Jiarui Zhao, the primary creator of the diary paper and a Ph.D. understudy at the Department of Physics.
“Mathematical reproductions have been a significant pattern in logical exploration of quantum materials. Our calculations and calculations could be seen as seriously fascinating and novel quantum matter, and such endeavors will definitely add to the advancement of both commonsense quantum innovation and the new worldview in key exploration, “said Dr. Zi Yang Meng, Associate Professor in the Department of Physics.
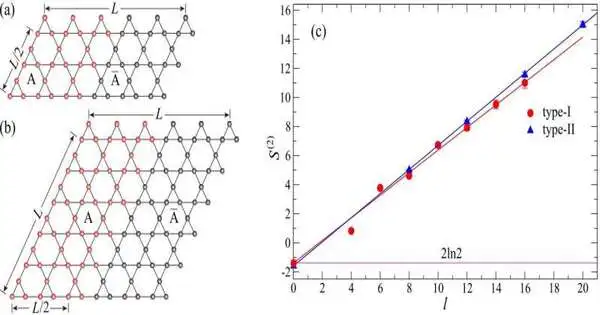
Figure 2: The grid types of the Kagome quantum turn model and the topological entropy comparison results.
The examination
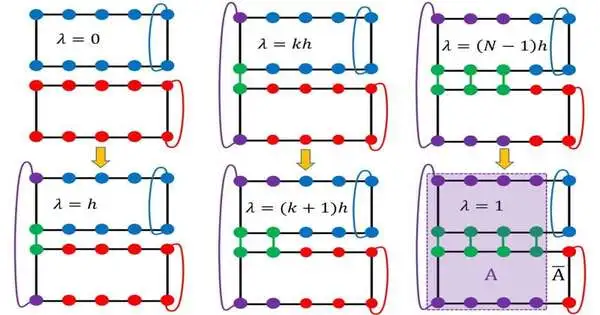
The group planned a mathematical examination on the Kagome turn model (Kagome is a two-layered grid structure that shows a comparable example to a customary Japanese woven bamboo design looking like hexagonal latticework) in the proposed QSL stage, and the schematic plot of the trial is represented in Figure 1. The ensnarement entropy (S) of a framework can be gotten by estimating the difference in the free energy of the model during a painstakingly planned nonequilibrium process. The topological entropy (), which describes long-range topological requests, can be removed by deducting the short-range commitment, which corresponds to the length of the entrapment limit (l), from the complete trap entropy (S), by fitting the information of snare entropy of various ensnarement limit lengths to a straight line (S=al-).
As displayed in Figure 2, the group led the examination on two sorts of grids with various proportions of length and width to guarantee the unwavering quality of the outcomes. The specialists utilized a straight line to fit the connection between the trap entropy and the length of the ensnarement limit, so the topological entropy ought to rise to the catch of the straight line. The outcomes give the worth of topological entropy to be 1.4(2), which is consistent with the anticipated worth of topological entropy of a Z2 quantum turn fluid, which is 2ln (2). The discoveries affirm the presence of QSLs according to a mathematical viewpoint.
More information: Jiarui Zhao et al, Measuring Rényi entanglement entropy with high efficiency and precision in quantum Monte Carlo simulations, npj Quantum Materials (2022). DOI: 10.1038/s41535-022-00476-0