A group of fictitious physicists from Finland’s University of Jyväskylä and Tampere University, as well as the Materials Physics Center in San Sebastian, Spain, explain how superconductors can transmit attractive data for significantly longer distances than ordinary metals. The discovery could be useful in data handling that makes use of appealing materials at low temperatures.
Isn’t it true that superconductors can transmit anything without warming up?
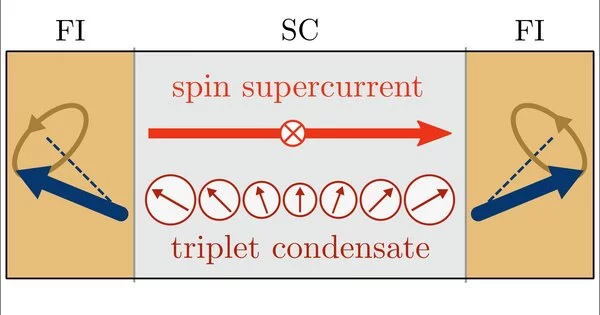
A few materials become superconductive at low temperatures, resulting in evaporating electrical resistivity. As a result, passing a charge current through a superconductor does not cause it to warm up. Electrons have different properties aside from charge. One of them is turn, which depicts the electron’s internal revolution around itself. In turn, the property is expected to grasp another type of material condition: attraction. Magnets and superconductors are rarely found in the same material. Regardless, attractive and superconducting materials can be placed close to one another and influence one another.
The new review, published in Physical Review Letters, demonstrates how, under certain conditions, superconductors can convey charge current between metals while also turning flows between magnets over moderately significant distances without delivering excessive heat. This is particularly interesting in common guides where such frictionless twist flows vanish within nuclear distances.
These twist flows can be used to controllably intervene in attractive communications between various magnets. They also appear in how magnets respond to external time-subordinate boosts, a feature that is particularly important in terms of attractive memory.
Because they do not deliver electric signs, such twist flows can be subtle. Regardless, they can be distinguished by the difference in their attractive setup. They do, however, fundamentally alter the attractive dynamical reaction. The analysts describe in the article the exploratory marks that show the presence of frictionless flows in both static and dynamic settings.
Risto Ojajärvi, who provided the itemized impact calculation, makes sense of: “Prior to our work, there was considerable uncertainty about the role of twist flows in superconductors, particularly how they work in balance.” We now present a composite image that depicts frictionless harmony flows in perfect balance with conventional flows that cause warming. “
The work explains how, on occasion, the presence of frictionless flows causes the entire framework to heat up more, rather than less, as would be naively anticipated. However, the warming occurs not in the superconductor that connects the magnets but in the magnets themselves, which can productively move between one another through the superconductor. This type of aggregate element is completely new, and it provides a broad perspective for designing dynamically attractive states.
Superconductors’ magnetic and electromagnetic properties
Basic field
One of the ways in which a superconductor can be constrained into the ordinary state is by applying an attractive field. The most vulnerable attractive field that will cause this progress is known as the basic field (Hc), assuming the example is a long, flimsy chamber or ellipsoid and the field is lined up with the long hub of the example. (In different arrangements, the example goes from the superconducting state into a transitional state, in which a few districts are typical and others are superconducting, and lastly into the ordinary state.) The basic field increments with decreasing temperature. The qualities (H0) of superconducting components range from 1.1 oersted for tungsten to 830 oersteds for tantalum.
These comments about the basic field apply to conventional (alleged type I) superconductors. In the accompanying segment, the behavior of other (type II) superconductors is analyzed.
The Meissner impact
As was expressed over, a sort of superconductor is a long, flimsy chamber or ellipsoid remaining parts superconducting at a decent temperature as a pivotally situated attractive field is applied, given the applied field doesn’t surpass a basic value (Hc). Under these circumstances, superconductors reject the attractive field from their inside, as could be anticipated from the laws of electromagnetism and the way that the superconductor has no electric obstruction. A seriously astounding impact happens assuming the attractive field is applied similarly to a similar sort of test at a temperature over the change temperature and is then held at a proper temperature while the example is cooled. It is observed that the example removes the attractive transition as it becomes superconducting. This is known as the Meissner impact. Complete removal of the attractive transition (a total Meissner impact) happens in this way for certain superconductors, called type I superconductors, yet just for tests that have the portrayed calculation. For tests of different shapes, including empty designs, a portion of the attractive transition can be caught, delivering a deficient or incomplete Meissner impact.
Type II superconductors have an alternate attractive way of behaving. Instances of materials of this sort are niobium and vanadium (the main kinds II superconductors among the synthetic components) and some composites and mixtures, including the high-Tc compounds. As an example, when a long, delicate chamber or ellipsoid is presented to a diminishing attractive field that is pivotally situated with the example, the increment of polarization, rather than occurring abruptly at the basic field (Hc), occurs gradually.Starting at the upper basic field (Hc2), it is finished at a lower basic field (Hc1; see Figure 2). On the off chance that the example is of another shape, is empty, or is inhomogeneous or stressed, some attractive motion stays caught, and some polarization stays after the applied field is totally taken out. The known upsides of the upper basic field stretch out up to 6 105 oersteds, the incentive for the compound of lead, molybdenum, and sulfur with the equation PbMo6S8.
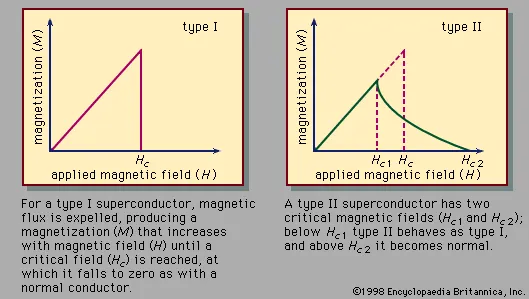
Image: Encyclopedia Britannica, Inc.
The ejection of attractive transitions by type I superconductors in fields underneath the basic field (Hc) or by type II superconductors in fields beneath Hc1 is never fully as complete as has been expressed in this work on show, on the grounds that the field generally enters into an example for a little distance, known as the electromagnetic entrance profundity. The advantages of the infiltration profundity for the superconducting components at low temperatures lie in the range from around 390 to 1,300 angstroms. As the temperature moves toward the basic temperature, the infiltration profundity turns out to be incredibly large.
High-recurrence electromagnetic properties
The previous depictions have dealt with the behavior of superconductors in the absence of electromagnetic fields or in the presence of constant or gradually changing fields; the properties of superconductors in the presence of high-recurrence electromagnetic fields have also been considered.
The energy hole in a superconductor straightforwardly affects the retention of electromagnetic radiation. At low temperatures, at which an irrelevant part of the electrons are thermally eager to state over the hole, the superconductor can retain energy just in a quantized sum that is something like two times the hole energy (at outright zero, 20). In the ingestion interaction, a photon (a quantum of electromagnetic energy) is consumed, and a Cooper pair is broken; the two electrons in the pair become energized. The photon’s energy (E) is connected with its recurrence () by the Planck connection, E = h, in which h is Planck’s steady (6.63 1034 joules per second). Henceforth, the superconductor can retain electromagnetic energy for frequencies as extensive as 20/h.
Transition quantization is appealing.
The laws of quantum mechanics dictate that electrons have wave properties and that the properties of an electron can be summarized in what is known as a wave function. On the off chance that a few wave capacities are in stage (i.e., they act as one), they are supposed to be cognizant. The hypothesis of superconductivity demonstrates that there is a solitary, rational, quantum mechanical wave function that decides the way of behaving of all the superconducting electrons. As an outcome, an immediate relationship can be shown to exist between the speed of these electrons and the attractive transition () encased inside any closed way inside the superconductor. To be sure, seeing that the attractive transition emerges as a result of the movement of the electrons, the attractive motion can be demonstrated to be quantized; i.e., the force of this caught transition can change exclusively by units of Planck’s constant, isolated by two times the electron charge.
Whenever an attractive field enters a sort II superconductor (in an applied field between the lower and upper basic fields, Hc1 and Hc2), it does so as quantized fluxoids, each conveying one quantum of motion. These fluxoids will generally organize themselves into normal examples that have been recognized by electron microscopy and by neutron diffraction. Assuming a sufficiently enormous current is flowing through the superconductor, the fluxoids move. This movement prompts energy dispersion that can warm the superconductor and drive it into the typical state. The greatest current per unit region that a superconductor can convey without being constrained into the ordinary state is known as the basic current thickness (Jc). In making wire for superconducting high-field magnets, producers attempt to fix the places of the fluxoids by making the wire inhomogeneous in synthesis.
Josephson currents
If two superconductors are isolated by a protecting film that shapes a low-obstruction intersection between them, observed Cooper matches can burrow from one side of the intersection to the next. (This interaction happens notwithstanding the single-molecule burrowing currently portrayed.) Thus, a progression of electrons, called the Josephson current, is created and is personally connected with the periods of the rational quantum mechanical wave work for all the superconducting electrons on the different sides of the intersection. It was anticipated that a few novel peculiarities ought to be recognizable, and tests have shown them. These are all collectively called the Josephson impact or impacts.
The first of these peculiarities is the entry of current through the intersection without any voltage across the intersection. The most extreme current that can stream at zero voltage relies upon the attractive transition () going through the intersection because of the attractive field created by ebbs and flows in the intersection and somewhere else. The reliance of the most extreme zero-voltage current on the attractive field applied to an intersection between two superconductors is displayed in Figure 3.

Credit: Encyclopedia Britannica, Inc.
A second type of Josephson effect is an oscillating current resulting from a relation between the voltage across the junction and the frequency () of the currents associated with Cooper pairs passing through the junction. The frequency () of this Josephson current is given by = 2eV/h, where e is the charge of the electron. Thus, the frequency increases by 4.84 1014 hertz (cycles per second) for each additional volt applied to the junction. This effect can be demonstrated in various ways. The voltage can be established with a source of direct-current (DC) power, for instance, and the oscillating current can be detected by the electromagnetic radiation of frequency () that it generates. Another method is to expose the junction to radiation of another frequency (′) generated externally. A graph of DC current versus voltage is discovered to have current steps at voltage values corresponding to Josephson frequencies that are integral multiples (n) of the external frequency (= n′); that is, V = nh′/2e. The observation of current steps of this type has made it possible to measure h/e with far greater precision than by any other method and has therefore contributed to our knowledge of the fundamental constants of nature.
Revelation and arrangement of high-temperature superconductors
Since the time Kamerlingh Onnes found that mercury becomes superconducting at temperatures under 4 K, researchers have been looking for superconducting materials with higher change temperatures. Until 1986, a compound of niobium and germanium (Nb3Ge) had the most elevated known progress temperature, 23 K, under a 20-degree expansion in 75 years. Most scientists expected that the following expansion experiencing significant temperature change would be found in a comparable metallic combination and that the ascent would be only a couple of degrees. In 1986, however, the Swiss physicist Karl Alex Müller and his West German partner, Johannes Georg Bednorz, found, following a three-year search among metal oxides, a material that had an exceptionally high melting temperature of around 30 K. They were granted the Nobel Prize for Physics in 1987, and their revelation quickly invigorated gatherings of agents in China, Japan, and the United States to deliver superconducting oxides with much higher melting temperatures.
These high-temperature superconductors are earthenware products. They contain lanthanum, yttrium, or one or more of the uncommon earth components, such as bismuth or thallium; barium or strontium (both antacid earth components); copper; and oxygen. Other nuclear species can be represented by synthetic replacement while still retaining high-Tc properties.
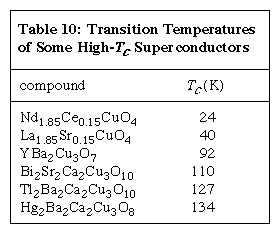
Table 10: Transition Temperatures of Some High-Tc Super Guides
The table shows which individual from each significant group of high-Tc materials has the highest noticeably superconducting change temperature. The value of 134 K is the most elevated realization of Tc esteem. Inside every group of high-Tc materials, just the addendums (i.e., stoichiometry) differ, starting with one compound, then onto the next. Tests in the families containing bismuth or thallium generally show a lot of nuclear issues, with particles in “some unacceptable” crystallographic locales and with debasement stages. It is conceivable that such an issue is expected to make these mixtures thermodynamically steady.
Designs and properties.
The mixtures have precious stone designs containing planes of Cu and O particles, and some likewise have chains of Cu and O iotas. The jobs played by these planes and chains have gone under extreme examination. Shifting the oxygen content or the intensity therapy of the materials decisively changes their progress temperatures, basic attractive fields, and different properties. Single gems of high-temperature superconductors are extremely anisotropic — that is, their properties related to a course, such as basic fields or basic current thickness, are profoundly dependent on the point between that bearing and the columns of molecules in the precious stone.
If the number of superconducting electrons per unit volume is privately disturbed by an applied power (typically electric or attractive), this unsettling influence spreads for a specific distance in the material; this distance is known as the superconducting cognizance length (or Ginzburg-Landau intelligibility length). Assuming a material has a superconducting locale and an ordinary area, large numbers of the superconducting properties vanish steadily—over a distance—after venturing out from the previous to the last district. In unadulterated (i.e., undoped) exemplary superconductors, is available for two or three thousand angstroms, whereas in high-Tc superconductors, it is available for one to ten angstroms. The small size of influences the thermodynamic and electromagnetic properties of the great Tc superconductors. For instance, it is liable for the cusp state of the particular intensity bend close to Tc that was referenced previously. It is also responsible for the ability of high Tc superconductors to remain superconducting in extremely large fields—at a million gauss (100 teslas) at low temperatures.
The high-Tc superconductors are type II superconductors. They show zero, areas of strength for opposition, the Meissner impact, attractive motion quantization, the Josephson impacts, an electromagnetic entrance profundity, an energy hole for the superconducting electrons, and the trademark temperature conditions of the particular intensity and the warm conductivity that have been portrayed previously. Thusly, the conduction electrons in these materials structure the Cooper pairs used to make sense of superconductivity in the BCS hypothesis. Accordingly, the focal points of the BCS hypothesis are illustrated. Without a doubt, that hypothesis directed Bednorz and Müller as they continued looking for high-temperature superconductors. It isn’t known, nonetheless, why the progress temperatures of these oxides are so high. It is by and large accepted that the individuals from a Cooper pair are bound together on account of cooperation between the electrons and the grid vibrations (phonons). However, it is impossible that these communications are sufficiently able to make sense of progress temperatures as high as 90 K. Most specialists accept that connections among the electrons create high-temperature superconductivity. The subtleties of this connection are challenging to treat hypothetically on the grounds that the movements of the electrons are emphatically associated with one another and on the grounds that attractive peculiarities have a significant influence in deciding the tiny properties of these materials. These solid relationships and attractive properties might be liable for surprising temperature conditions of the electric resistivity and Hall coefficient RH in the typical state (i.e., above Tc). (For a discussion of the Hall impact, see the attraction: Magnetic powers.) It is seen that at temperatures above Tc, the electric resistivity, albeit higher for superconductors than for common metals in the ordinary state, generally corresponds to the temperature T, a surprisingly frail temperature dependence. Estimations of RH demonstrate it to be fundamentally temperature-subordinate in the typical state (in some cases corresponding to 1/T) as opposed to being generally autonomous of T, which is the situation for standard materials.
Applications
Movies of the new materials can convey flows in the superconducting state that are adequately huge to be of significance in making numerous gadgets. The development of PC parts (rational gadgets, memory components, switches, and interconnects), oscillators, intensifiers, molecule gas pedals, profoundly touchy gadgets for estimating attractive fields, voltages, or flows; magnets for clinically attractive imaging gadgets; attractive energy-stockpiling frameworks; suspended traveler trains for high velocity travel; engin The chief benefits of these superconducting gadgets would be their low power dispersion, high working rate, and outrageous awareness.
High-temperature superconductors would also be less expensive to work with because they can be cooled with cheap fluid nitrogen (limit, 77 K) rather than expensive fluid helium (edge of boiling over, 4.2 K). In any case, there are issues with earthenware production that must be resolved before useful gadgets can be produced using them. These issues include material fragility, material dangers under certain conditions, and a proclivity for contaminations to isolate at surfaces and grain boundaries, where they impede the progression of high flows in the superconducting state.
Donald M. Ginsberg